Rain in Codelandia: Solution

Problem: Rain in Codelandia
Challenge: Harder
Concepts: Logic, Loops
Download: rain-in-codelandia-solution.zip

This is a tricky problem — not because the code itself is hard, but finding the right algorithm can take a while.

The amount of rain a building will catch can be found by finding the highest building to its left (include itself in that finding) and by finding the highest building to the right (again, include itself).

Whichever of those numbers is smaller is our “leak level”; the amount of rain a building captures is it’s leak-level minus it’s height.

For example:

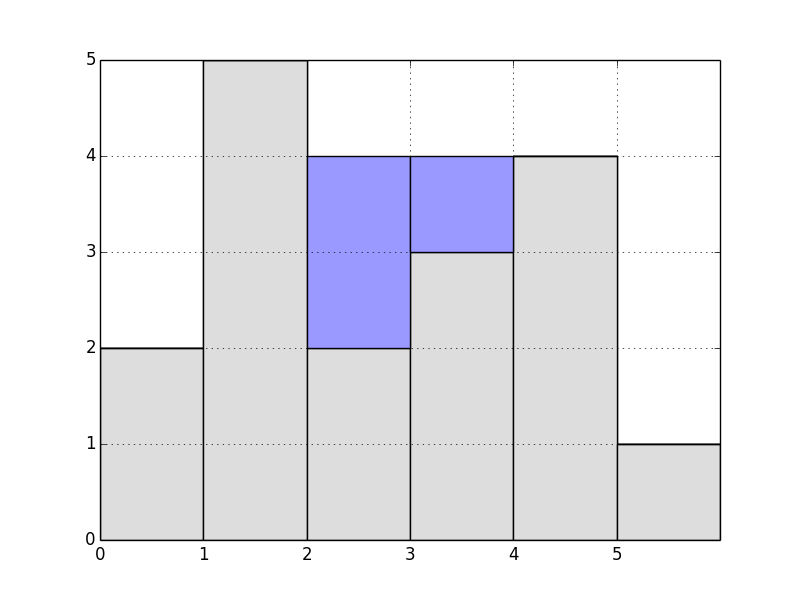
For each building:

2: it’s highest-left is 2 (remember, include itself) and it’s highest-right is 5. Our leak level (min of those two numbers) is 2, so its captured rain is 2 - 2 == 0.
5: highest L/R is 5,5; leak level is 5, rain is 5 - 5 == 0.
2: highest L/R is 5,4; leak level is 4; rain is 4 - 2 == 2.
3: highest L/R is 5,4; leak level is 4; rain is 4 - 3 == 1.
4: highest L/R is 5,4; leak level is 4; rain is 4 - 4 == 0.
1: highest L/R is 5,1; leak level is 1; rain is 1 - 1 == 0.

Our total rain captured is the sum of that: 0 + 2 + 1 + 0 + 0 == 3.

The code for this is relatively straightforward:

rain.py

def rain(buildings):
    """How much rain is trapped in Codelandia?"""

    # START SOLUTION

    rain = 0

    # Special case: no buildings means nothing trapped

    if not buildings:
        return rain

    for i, height in enumerate(buildings):

        # Find highest building to our left (including us)
        left_best = max(buildings[:i + 1])

        # Find highest building to our right (including us)
        right_best = max(buildings[i:])

        # The shorter of these is "leak level"; rain is our height to that

        leak_level = min(left_best, right_best)
        rain += leak_level - height

    return rain

The runtime for this is O(n ** 2) — we have a outer loop over all buildings and, for each building, we scan the list looking our best-left and our best-right.

Advanced: Linear Runtime

There is a linear solution for this problem, though it’s tricky to find.

Take a look at the list above of best-left and best-right values: once we find that 5 in the list, it remains the best-left for every building after that. Similarly, going right-to-left, once we find that 4, it remains that best-right for every building before it.

Instead of having to find the best-left and best-right every time we loop, we can do two simple linear passes over the buildings, finding the best-seen-so-far going left, and best-seen-so-far going right. The can both be done with this function:

rain.py

def highest_so_far(buildings):
    """Returns list of highest-building-seen-so-far for each building."

    For example::

        >>> buildings = [1, 3, 2, 5, 2, 1]

    This is "list of 'highest building to my left'"::

        >>> highest_so_far(buildings)
        [1, 3, 3, 5, 5, 5]

    You can use this to get rightward answer by reversing input & result
    (this is "list of 'highest building to my right'")::

        >>> list(reversed(highest_so_far(reversed(buildings))))
        [5, 5, 5, 5, 2, 1]
    """

    so_far = 0
    out = []

    for height in buildings:
        so_far = max(height, so_far)
        out.append(so_far)

    return out

With these lists in hand, our rain function is very similar, except it can just use these already-calculated lists, rather than making a new one each time. This reduces the inner loop, making this linear:

rain.py

def rain_linear(buildings):
    """How much rain is trapped in Codelandia?"""

    rain = 0

    # Special case: no buildings means nothing trapped

    if not buildings:
        return rain

    # The amount of rain caught by a building is defined by
    # its highest-building-ever-on-the-left and
    # its highest-building-ever-on-the-right.

    # Make lists of highest-left and highest-right

    highest_on_left = highest_so_far(buildings)
    highest_on_right = reversed(highest_so_far(reversed(buildings)))

    for height, best_l, best_r in zip(buildings, highest_on_left, highest_on_right):
        leak_level = min(best_l, best_r)
        rain += leak_level - height

    return rain

Alternate Solution

Here’s another linear solution that takes a more physical approach. Imagine filling up the box that bounds the buildings, ie, height equal to the tallest building and width equal to the length of the list of buildings. Then we need to calculate how much water will run off to the left and the right. Note that any particular element of water can only drain to one side because the tallest building(s) will not allow water to pass. The amount of water remaining is simply the initial amount minus the runoff.

The calculation of runoff to one side is relatively straightforward. We need only keep track of the tallest building encountered so far as we proceed from one side, hence the space complexity of this solution is constant.

rain.py

def rain_linear_alternate(buildings):
    """How much rain is trapped in Codelandia?"""

    if not buildings:
        return 0

    top = max(buildings)  # height of tallest building

    runoff = 0

    # amount of water that runs off to the left
    highest = 0
    for height in buildings:
        if height == top:  # no more water will drain to the left
            break
        highest = max(highest, height)
        runoff += top - highest

    # amount of water that runs off to the right
    highest = 0
    for height in reversed(buildings):
        if height == top:
            break
        highest = max(highest, height)
        runoff += top - highest

    # trapped water = area of bounding box - area of buildings - total runoff

    return top * len(buildings) - sum(buildings) - runoff