Rain in Codelandia

Challenge

Harder

Concepts

Logic, Loops

Download

rain-in-codelandia.zip

Solution

Rain in Codelandia: Solution

The city of Codelandia is densely packed and in a very rainy climate.

You can imagine the skyline of the city packed with buildings like this:

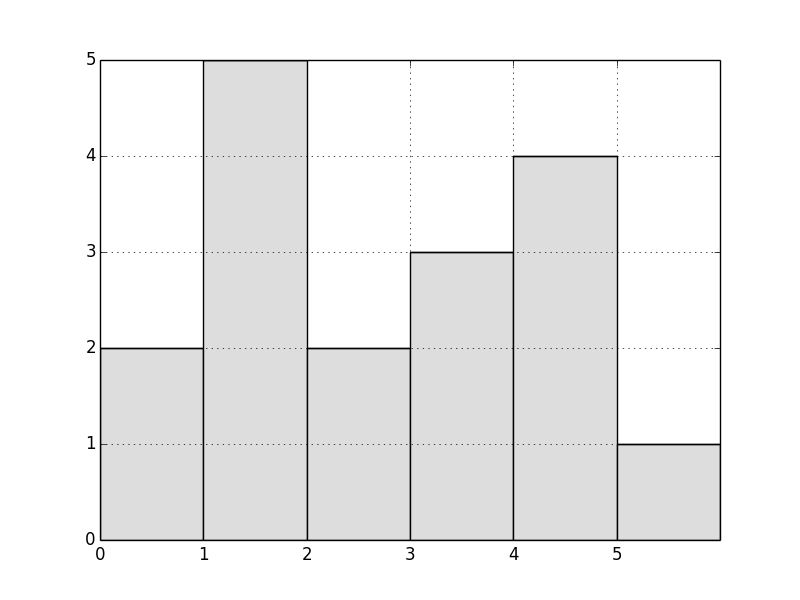
Each building is exactly 10 feet wide, and each floor is exactly 10 feet tall, though the number of floors (and therefore, the effective height) varies for each building.

In this challenge, you want to figure out how much rain would be trapped on top of buildings. The building roofs are 100% leakproof, and there’s no space between buildings.

For the city above:

• the leftmost building doesn’t gather any rain; it would just run off the left edge

• the 2nd building doesn’t gather any rain itself; it’s taller than everything else

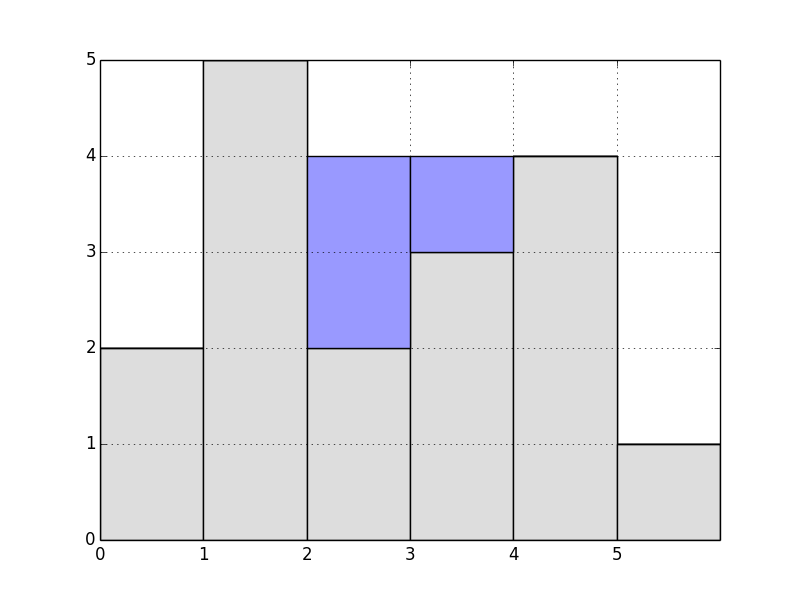
• the 3rd building holds 2 squares of rain

• the 4th building holds 1 square of rain

• the 5th building doesn’t gather any rain itself; it would run off its right edge

• the 6th building doesn’t gather any rain itself; it would run off its right edge

So, the rain gathered looks like this:

def rain(buildings):
    """How much rain is trapped in Codelandia?"""

Test Cases

No buildings mean no rain is captured:

>>> rain([])
0

All-same height buildings capture no rain:

>>> rain([10])
0

>>> rain([10, 10])
0

>>> rain([10, 10, 10, 10])
0

If there’s nothing between taller buildings, no rain is captured:

>>> rain([2, 3, 10])
0

>>> rain([10, 3, 2])
0

If two tallest buildings are same height and on ends, it’s easy:

>>> rain([10, 5, 10])
5

>>> rain([10, 2, 3, 4, 10])
21

>>> rain([10, 4, 3, 2, 10])
21

>>> rain([10, 2, 4, 3, 10])
21

If two tallest buildings are ends, but not the same height, it will fall off the shorter of the two:

>>> rain([10, 2, 3, 4, 9])
18

Rain falls off the left and right edges:

>>> rain([2, 3, 10, 5, 5, 10, 3, 2])
10

Trickier:

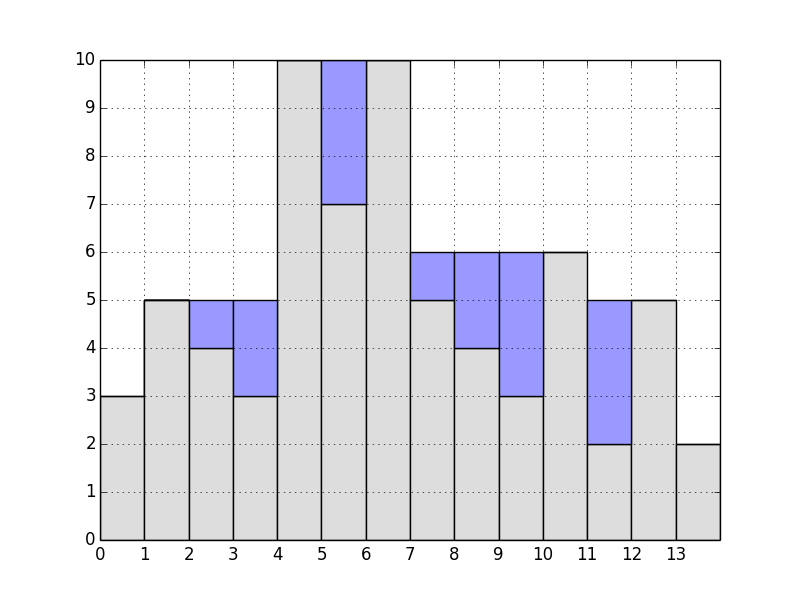
>>> rain([3, 5, 4, 3, 10, 7, 10, 5, 4, 3, 6, 2, 5, 2])
15

If it helps, here’s a visualization of that last case:

Good luck!