Same Line

Whiteboard: Harder
Challenge: Medium
Concepts: Loops, Geometry
Download: sameline.zip
Solution: Same Line: Solution

In this challenge, you will write a function that finds points that fall on a line with at least 3 points (it wouldn’t be very challenging to find points that fall on a line with at least 2 points as any two points form a line!).

Imagine the set of x, y points:

[ (0,0), (1,1), (2,3), (3,2), (3,3), (3,4) ]

We could plot these:

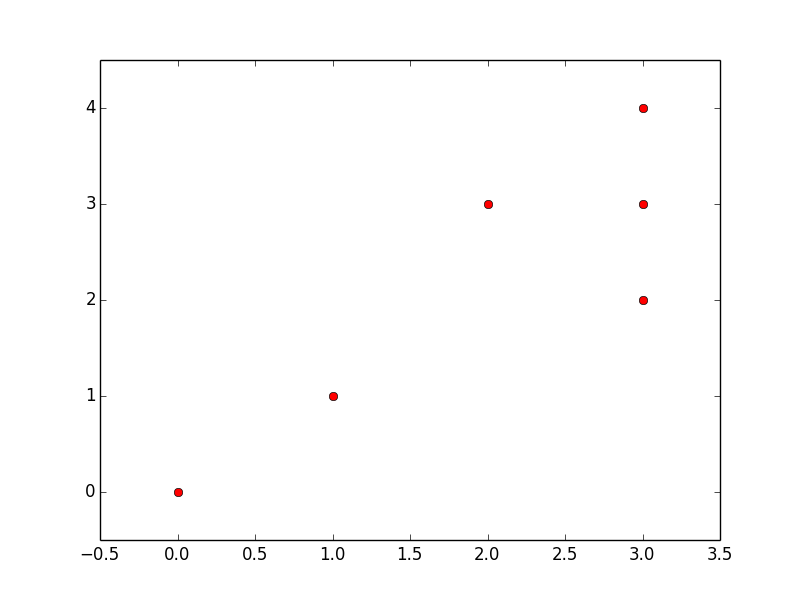
Six of these points are on lines that involves more than two points (in this graph, these points are shown on the red and green lines):

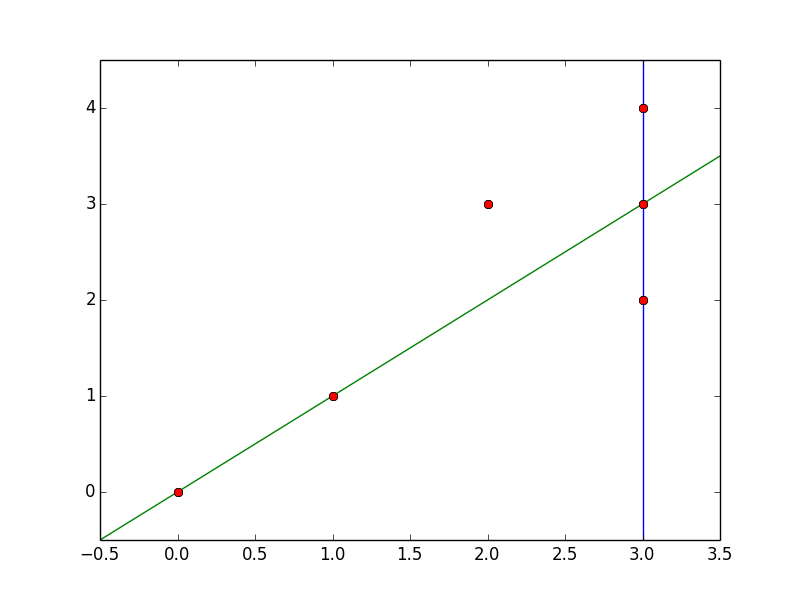
The points in our list that fall on those lines are:

[ [(0, 0), (1, 1), (3, 3)],
  [(3, 2), (3, 3), (3, 4)]
]

Your challenge is to write function that is given a list of x, y tuples of points, and returns a list of lines, showing only lines with more than 3 points on it. The lines themselves should be a list of points that fall on that line.

We’ve written a function, sameline. Implement it:

sameline.py

def sameline(pts):
    """Find segments comprising >2 points."""

Hint

Combinations

Python has a library, itertools with a function in it, combinations, which finds all combinations of an iterable.

For example, you could use this to find all 3-letter ways to combine the letters “abcd”:

>>> import itertools
>>> list(itertools.combinations("abcd", 3))
[('a', 'b', 'c'), ('a', 'b', 'd'), ('a', 'c', 'd'), ('b', 'c', 'd')]

This may be very useful for your solution.

(A “combination” is different than a “permutation”; permutations consider order significant, so “abc” is different permutation than “cab” but is the same combination.)

Tests

There are no 3+ segments here:

>>> sameline([(0, 0), (1,1), (3,2), (4,3)])
[]

There are two 3+ segments here:

>>> sameline([(0,0), (1,1), (2,3), (3,2), (3,3), (3,4)])
[[(0, 0), (1, 1), (3, 3)], [(3, 2), (3, 3), (3, 4)]]